When Jupiter Blazed Over Babylon
- Douglas MacDougal
- Sep 28, 2024
- 18 min read
Updated: Jan 25
As Jupiter burns brightly in our night sky this month, our thoughts turn to how this great, brilliant beacon must have appeared twenty two centuries ago in the pitch-dark skies over Babylon. The ancient Babylonians sought mightily, almost obsessively, to foretell exactly the where and when of its arrivals in the sky. That effort was the very beginning of computational astronomy and the first step in what we now call the scientific method.
Most would agree that the method of science in any era begins by asking questions about the natural world, finding a way of quantifying what one sees, and (if possible) recording one’s conclusions. If this is so, then the Babylonians were unquestionably the first scientists of the sky. So much lay above them worth noting they couldn’t stop scribbling about it. No nuance of heavenly motion escaped their attention. Observing from atop their great ziggurats in Babylon and Uruk, they documented every relevant jot, whit, and nuance of lunar and planetary happenings day by day for weeks, months, centuries. It was perhaps the most extraordinary case of continuous record keeping in human history. Their records, known to us through thousands of broken tablet fragments, were inscribed in tiny, furiously crimped cuneiform characters in a language long dead yet miraculously deciphered by a century of painstaking scholarship. Judging by the sheer volume of those records, all strewn with numbers, it is easy to believe how mysterious and captivating the subtle movements of the moon and planets must have been to these first astronomers.
All this contrasts remarkably with the habits of the ancient Egyptians who seemed to have had little interest in practical or computational astronomy. As a teenager I was lucky enough to see the temples, tombs, and pyramids of Egypt decorated with their beautiful hieroglyphics, some of which still retain traces of color. Writing was everywhere, on almost every flat or curved surface. I was so enchanted by it that I later took a course on Egyptian hieroglyphics from the University of Chicago’s Oriental Institute (I still have my Egyptian grammar books!) – now called the Institute for the Study of Ancient Cultures. But despite the beauty and uniqueness of that ancient culture, as to astronomy, one will find very little. “Among the enormous mass of Egyptian inscriptions and papyri from all periods of Egyptian independent history there has not been found a single record of astronomical observations,” wrote antiquities scholar Otto Neugebauer [1]. Mesopotamia, though, was unique: “Nowhere within ancient civilizations known to us did the sciences originate independently … with the sole exception of Mesopotamia [2].”
The Babylonians all the while watched the skies intently and inscribed their findings in the less charismatic symbols and logograms of Akkadian cuneiform. And if science progresses further by the discovery of mathematical relationships buried within the accumulated heaps of such records, then the Babylonians took this early step too, embarking on the bold experiment of mathematically modeling phenomena to aid their predictions. The Babylonians indeed were the first computational astronomers in western history, and their legacy is apparent in works written many centuries later.
Ancient skywatchers
It was the task of the Babylonian astronomer-priests to predict when and where in the sky the planets (and the moon) would appear and reappear, and thus to read the celestial omens that foretold the fate of the king and society. Initially interested in discerning omens, over time the work of the Babylonian astronomer priests became an end in itself, “no longer religious but purely technical,” in the words of historian of science George Sarton: “They began as priests; they ended as astronomers or perhaps mathematicians.” There is much evidence that supports this case [3]. Here we take only a small piece of that great picture, and turn to one of the Babylonian astronomers’ most vexing problems – an ancient precursor to modern celestial mechanics – of knowing in any year exactly where and in what constellation Marduk's great star Jupiter would brilliantly return to their desert skies.
One of their first technical achievements was to focus on a quantity which when known seems to have unlocked for them a whole vault of planetary knowledge. That quantity was the synodic period of a planet or the moon. You may recall from our earlier posts about Mars [4], that a planet’s synodic period is measured by how many years and days must pass before the planet would return to exactly (or nearly exactly) the same place in the sky as it was at its previous occurrence [5]. The ancients tracked five synodic events for the outer planets: heliacal rising, first station, opposition, second station, and heliacal setting [6]. The ‘stations’ are the places where the planet appears to stop in the sky and change direction, in a retrograde loop, as (for outer planets) the earth in its quicker orbit approaches and overtakes the slower outer planet. We are most familiar with oppositions, where Mars or Jupiter or Saturn (the only outer planets then known) stand directly opposite the sun: when the planet will rise with the setting sun and shine brilliantly overhead at midnight [7].
The Babylonians knew the mean synodic periods precisely. But knowing the mean value of anything will rarely tell you what its actual value will be on this day or that, or this year or that. Jupiter, they discovered, moves at a slower pace in some parts of its orbit than in others. This presented thorny challenge for Babylonian scholars to account for in their long-term ephemerides (i.e., tables, in format somewhat like railroad schedules, that list predicted lunar or planetary positions for future dates and times).
Tracking Marduk’s star
Jupiter was the manifestation of the Babylonian god Marduk, their great and powerful deity (logogram 𒀭𒀫𒌓). Its appearance was seen as a positive omen. “When the star of Marduk appears at the beginning of the year, in that year corn will be prosperous,” reads one tablet inscription [8]. It was vital to track it accurately, and foretell when and where it would appear. If we travel back in our minds twenty-two centuries, we can imagine the early astronomers spotting Jupiter, say, in Gemini, and hear them asking, “When was it there before?” "When will it return?" Consulting their tablet files, they’d note it was there about 12 years earlier but slightly behind where it was expected to be. And it was also there 71 years ago, but a little ahead. And they’d look back still further to confirm that these sightings with their errors were repeated 24, and 142 years ago. But how, without telescopes, instruments, or any sort of advanced mathematics, could they have gone beyond these basic impressions?
One answer must begin with the phenomenal completeness of their observations. Cuneiform tablets from Babylon and Uruk in the second century BCE are among the most complete [9] and detail Jupiter's position through many decades of continuous observations [10]. With this trove of information, scholars have been able to track Marduk's star through its orbit as the Babylonians did and reconstruct what they were able to learn [11].
We know from those records that “exact periods” were fashioned from combinations of shorter periods chosen so their known errors would cancel out. Procedure texts were found which even tell us how computations were to be performed – fortuitous ‘rule books’ if you will, of enormous benefit to the scientific code breakers of the future. They reveal several synodic periods of Jupiter. Measured against the Babylonians' catalog of fixed stars, however, each had errors [12]. Two Jovian synodic periods, of 12 years and 71 years, require corrections of +5° and − 6°, respectively, for a return to the same sidereal longitude (i.e., place in the sky as before) [13]. To net out the errors (by the same method as we noted in our Mars article), the Babylonians combined 6 of the 12 year periods (for + 30⁰ accumulated error) and 5 of the 71 year periods (for − 30⁰ accumulated error). The result, with the errors zeroed out, is that a perfect return should occur after
6 · 12 + 5 · 71 = 427 years
Hence, two periods, each less than one century long, could be used with remarkable ingenuity to construct a period which should be "exact" for more than four centuries, far beyond any actual period of continuous observation [14]. It is very accurate! The orbital period implied by this data is 11.86 years, consistent with the modern value [15].
Shifting constellations
We can also envision the Babylonians noticing that in the shorter term, from year to year, Jupiter’s opposition place in the sky would on average shift eastward by about 33 degrees. Since there are 12 constellations in the 360-degree arc of the zodiac, each constellation on the map is 30 degrees apart. Jupiter therefore moves on average just a whisker more than a full constellation’s distance between oppositions. But here too deviations arose, something was amiss: tablet records showed that in some years the arc distance was greater and in some it was less. Why was this [16]?
This angular distance is called the mean synodic arc and represents the average eastward shift in degrees in the sky from one planetary opposition to the next. Accurately knowing the synodic arc of a planet helped tell the Babylonians where in the sky a planet would be in its next opposition, more or less by leapfrogging arc by arc from one opposition to the next [17]. But because Jupiter moves faster in one part of its orbit than another, applying the mean ~ 33 degree synodic arc to find out where it would be next didn't work. We know why that is, but they did not. It happens because Jupiter (as with the other planets) travels around the sun in an elliptical orbit, with the sun at one focus of the ellipse, an epic discovery made by Johannes Kepler in 1609 [18].
To account for the planet’s changes of speed, the Babylonians divided Jupiter’s orbit into a slow part and a fast part: its orbit now consisted of a slow arc (applicable to one part of its orbit) plus a fast arc (applicable to the other). This division the Jovian orbit into two arcs has been called System A by scholars [19]. Tablets reveal that for this two-zone System A, the Babylonians computed the fast arc for Jupiter to be 36⁰ and the slow arc to be 30⁰ [20]. These were the extremes against a computed mean synodic arc of 33;8,44,8⁰ (33.1457⁰).
A tablet tells a story
A while ago I had the idea of analyzing a sample tablet from Uruk that appears translated in Otto Neugebauer’s, A History of Ancient Mathematical Astronomy [21], so we could see for ourselves how the Babylonians quantified the synodic arcs for Jupiter's first station. Written in Uruk in S.E. (Seleucid Era ) 118, the Uruk tablet lists sixty years of the Seleucid Era, from S.E. 113 to 173, or calendar years -199 to -138 [22]. These are predicted events.
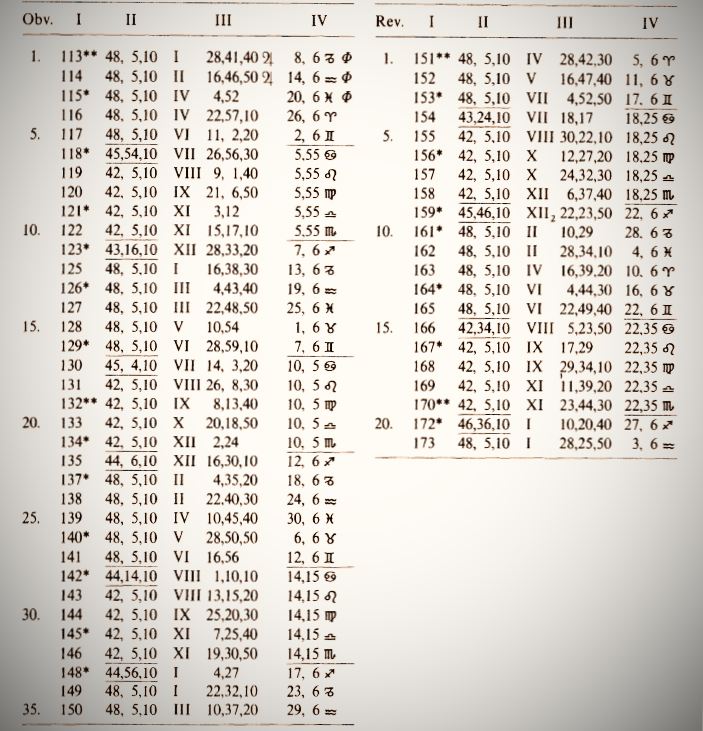
I had considered only a small subset of tablet data, Seleucid Era dates 113 to 140, and plotted the dates (as given on column I of the tablet) along the x axis, and the synodic arcs (as computed from the row-by-row differences in column IV of the tablet) along the y axis. My plot showed the expected 30-to-36-degree variation in the arcs.
For confirmation, I sent it (along with a draft of this article) to Dr. Teije de Jong of the Anton Pannekoek Astronomical Institute of the University of Amsterdam. His data squared with what I found, but he thought it would be clearer to combine, all in one graph, the old Babylonian year-by-year measurements with the true positions of Jupiter during those dates. It was an excellent idea. He generously created the graph below which combines the two kinds of data.
De Jong's figure compares the true astronomical variation of the synodic arc of Jupiter during S.E. 113 - 140 with the Babylonian system A values shown in the tablet figure. The plotted data reveal the 30-to-36-degree variation in the arcs.
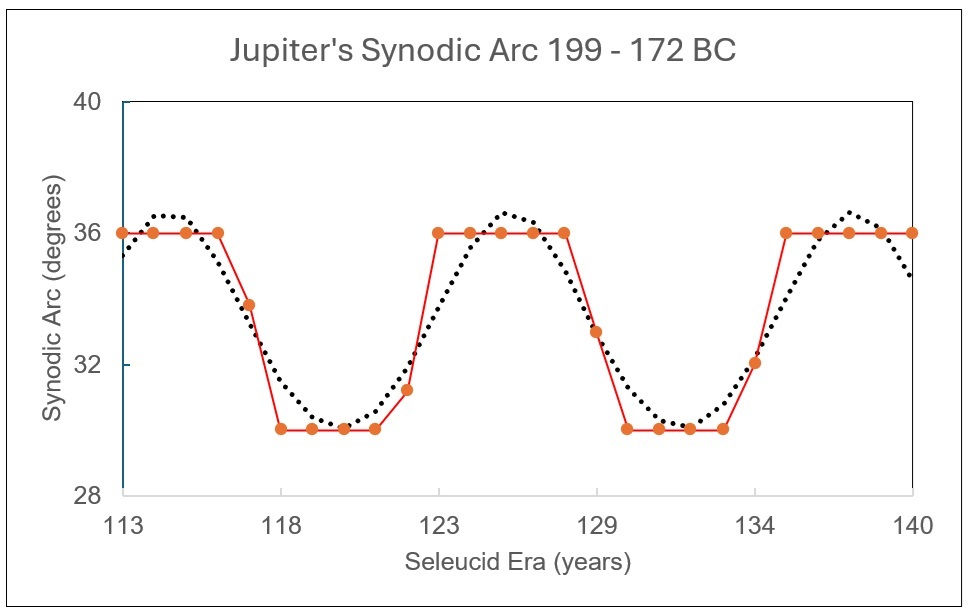
The quite congruent plots also show in a clear way how accurate the Babylonian predictions were.
If one were to trace through the tablet notations (as we do in the next article), one would notice that the fast arc (the 36º portion) begins at the constellation Sagittarius (at 240º ecliptic longitude) and runs to about 25º into Gemini (85º ecliptic longitude); the slow arc (the 30º portion) from there back to Sagittarius [23], consistent with Babylonian procedure texts. Later, the Babylonians divided the arcs into four parts to try to “smooth” the transitions. This became known as System A’ [24].
We know Jupiter’s speed doesn’t abruptly change as it sojourns on its almost 12-year path around the sun, but rather varies gradually, as seen in the dotted, sinusoidal curve of the graph. Yet this division of its orbit into different arcs was a remarkable first step for an ancient culture, to in effect model its orbit, albeit roughly, to better conform their predictions to Jupiter’s actual movements.
We do not use synodic arcs in modern celestial mechanics. Since Newton’s discovery of the universal the law of gravitation, its equations are effective and sufficient to model orbital dynamics – precise enough to guide spacecraft to exact orbits even around the distant planets. But though you won’t find computer models of synodic arcs in celestial mechanics books, knowledge Babylonian goal years and synodic arcs is beautifully useful to anyone wishing to intuit planetary motions and returns as the ancients did [25].
This and other well-known achievements of the Babylonians – the Saros cycle, the sexagesimal number system, the 360° ecliptic, the named constellations – became part of the Babylonian scientific heritage passed on to the Greeks and later civilizations. These gifts from Babylonian culture undoubtedly inspired a growing belief in the possibility of a rational universe, firmly demonstrated by mathematics and the beauty of its results, that the movements of the sun, moon, and planets could be accurately predicted and thus tamed by the mind of man.
Appendix: (More) Babylonian Math on Your Calculator [26]
We can see how the average synodic arc for Jupiter could be mathematically derived from the planet’s ‘exact’ period. From Babylonian tablets, the ancients knew that Jupiter’s exact period of 427 years constitutes 36 revolutions of Jupiter around the sun (the revolutions typically signified by the letter Z in the literature), during which there will be (427 – 36 =) 391 synodic occurrences (often signified by the Greek letter Π in the literature) [27]. Jupiter thus experiences these 391 synodic occurrences over the course of 36 complete 360⁰ rotations around the ecliptic, or during a total of (36 · 360 =) 12,960⁰ of revolutions. That means each synodic occurrence is about (12,960/391 =) 33.1457⁰ apart in the sky, on average, from the previous one. (Imagine a large spiral of 36 turns with 391 markers on it, each marker representing an opposition, spaced about 33⁰ of arc apart.) This spacing is Jupiter’s mean synodic arc, and appears on tablets in sexagesimal notation as 33;8,45 [28].This means that Jupiter should on average shift east along the ecliptic by a little more than 33⁰ every 399 days (Jupiter’s synodic period).
Note on the header image
The images are the Akkadian logogram for the Babylonian god Marduk at the top; a Babylonian astronomical tablet fragment; partial transliteration of the Uruk tablet referred to in the text; and the symbols for the signs of the zodiac.
Acknowledgment
I wish to thank Dr. Teije de Jong of the Anton Pannekoek Astronomical Institute of the University of Amsterdam for his helpful comments on an earlier draft of this article and for his exceptionally generous contribution of the above graph.
References:
Clarke, Leonard W. “Greek Astronomy and its Debt to the Babylonians.” British Journal for the History of Science 1, no.1 (June 1962): 65-77. https://www.jstor.org/stable/4025075.
de Jong, Teije. 2018. A Study of Babylonian Planetary Theory I. The Outer Planets. Archive for History of Exact Sciences (2019) 73:1–37. https://doi.org/10.1007/s00407-018-0216-0.
Jones, Alexander. 2007. A Portable Cosmos: Revealing the Antikythera Mechanism, Scientific Wonder of the Ancient World. Oxford: Oxford University Press.
Lindberg, David C. 2007. The Beginnings of Western Science: The European Scientific Tradition in Philosophical, Religious, and Institutional Context, Prehistory to A.D. 1450. Chicago: The University of Chicago Press.
Neugebauer, O. 1975. A History of Ancient Mathematical Astronomy. 3 vols. Studies in the History of Mathematics and Physical Sciences 1. Berlin: Springer (cited as HAMA).
_________. (1957) 1969. The Exact Sciences in Antiquity. Reprint, New York: Dover Publications, Inc.
_________. 1955. Astronomical Cuneiform Texts. Sources in the History of Mathematics and Physical Sciences 5. Berlin: Springer (cited as ACT).
Pannekoek, A. (1951) 1961. A History of Astronomy. Reprint, New York: Dover Publications, Inc.
N. A. Roughton, J. M. Steele, C. B. F. Walker. “A Late Babylonian Normal and Ziqpu Star Text.” Arch. Hist. Exact Sci. 58 (2004): 537–572. https://doi.org/10.1007/s00407-004-0083-8.
Sarton, George. “Chaldaean Astronomy of the Last Three Centuries B.C.” Journal of the American Oriental Society 75, no. 3 (July - September 1955): 166-173.
Sachs, A. “A Late Babylonian Star Catalog.” Journal of Cuneiform Studies 6, no.4 (1952): 146-150. https://www.jstor.org/stable/1359538.
NOTES
[1] HAMA, 560. “Egypt provides us with the exceptional case of a highly sophisticated civilization which flourished for many centuries without making a single contribution to the development of the exact sciences.” Ibid, 559.
[2] HAMA 559. The full quote is: “Nowhere within ancient civilizations known to us did the sciences originate independently, neither in pre-Hellenic nor in early Greek civilization, in the ancient Near East, on the Iranian plateau, nor in pre-Arian or Arian India - with the sole exception of Mesopotamia, probably in the early second millennium. It is at this single center that abstract mathematical thought first appeared, affecting, centuries later, neighboring civilizations, and finally spreading like a contagious disease.”
[3] The quote is from Sarton, 170. For an introduction to the scientific evolution of the Babylonian culture, see Lindberg, 12-20; Neugebauer (1957), Chaps. II and V; Pannekoek, Chaps. 1 - 6; Sarton; Clarke. For a deep dive into the mathematical details, see HAMA Book II.
[4] See my post, A Farewell to Mars, June 14, 2021, for a glossary of some terms used in this article and some applications. For an explanation of Babylonian methodology using Mars as the context, see my post of October 1, 2020, Alas Babylon! Mars Draws Near, and my August 2021 Sky & Telescope magazine article of the same title. For more emphasis on the computational methods, see my journal article, “Exploring the Mysteries of Babylonian Astronomy with Maple.” Maple Transactions, September 2022, a journal of computational mathematics, cited as Maple Trans. 2, 1, Article 14357 (2022).
[5] Every type of synodic event recurs at intervals of the same synodic period. In other words, the mean time interval between oppositions will be the same as the mean time interval between each of the other synodic events mentioned in the text.
[6] The five planetary phenomena for the outer planets of most interest to the Babylonian astronomers were the heliacal rising, first station, opposition, second station, and heliacal setting. Otto Neugebauer has referred to these events as “Greek letter phenomena.” HAMA, 386 and note 11 below. He refers to heliacal risings and settings as “reappearance after invisibility,” and “disappearance.” That is, when a planet first emerges from the glare of the sun in the early morning, and when it is lost in the glare of the sun in the early evening. He emphasizes that the Babylonians were concerned about these events, these planetary phases, and not anything in between, at least not until they later began to develop ephemerides.
[7] Though discussion of synodic periods often focus on the easiest-to-grasp oppositions, the term synodic applies to any phenomena that depends on the relative location of the planet, earth and sun. The synodic phenomena tracked by the Babylonians for the outer planets are discussed in note 6.
[8] Pannekoek, 39. See also, Jones, 163.
[9] “Among the ephemerides assembled in ACT [Astronomical Cuneiform Texts] Jupiter is by far the best represented planet.” HAMA, 441.
[10] Otto Neugebauer describes the fascinating variety of tablet sources of our knowledge of Babylonian astronomy in HAMA, 351-353.
[11] HAMA, 398. “We have ample textual evidence for ephemerides which concern the whole set of Greek-letter phenomena [for Jupiter] in their natural order." Otto Neugebauer’s “Greek letter phenomena” are his shorthand for the synodic events of the planets. The five he describes for the outer planets are: Γ reappearance after invisibility; Φ first station; Θ opposition; Ψ second station; and Ω disappearance. HAMA, 386. “S.E.” stands for Seleucid era, referred to in note 22.
[12] HAMA, 391. The measurements were made against a catalog of so-called (by scholars) “Normal Stars” found in “Normal Star Almanacs.” HAMA, 391 & 555. For interesting discussions on the Normal Star catalogs and their sources, see Sachs and also Roughton et al.
[13] HAMA, 391. See also de Jong, 7, who has himself computed the errors for the 12- and 71-year periods of Jupiter to be +5 and – 6 days (rounded) respectively.
This type of accounting sometimes confuses people. Think of it this way: In 12 years we expect the synodic arcs to have accumulated to ~ 397.75°, since they advance a mean arc of 33.1457° per synodic cycle. One ‘set’ of the synodic arc is (I define as) a full revolution plus the mean arc length: (360 + 33.1457) = ~ 393.15°. So, in 12 years we expect Jupiter to have gone slightly less than one set of mean arcs, being off by about −5°. Hence the correction needs to be plus that. In 71 years, we expect the synodic arcs to have accumulated to ~ 2,353°, since they advance 33.1457° per cycle. But six arc sets = ~ 2,359°. So, in 71 years Jupiter has progressed slightly more than a set of six perfect arcs by about +6°. Hence the correction needs to be minus that amount.
[14] HAMA, 391. Actually, three periods have been attested for Jupiter, 12, 71, and 83 years, with errors (rounded) of +5, -6, and -1 days, respectively. De Jong, 6-7. The 71- and 83-year periods are “goal year” periods, mentioned in my earlier Mars articles (note 4). Note that the 83-year period is the sum of the other two (and hence yields the net error of -1). De Jong shows at least six combinations of those periods whose errors cancel and generate the exact period of 427 years. The Babylonian method of error cancellation to arrive at an exact period also appears to have been used for Mars. See HAMA, 426-427 and sources in note 4.
[15] See, e.g., https://nssdc.gsfc.nasa.gov/planetary/factsheet/jupiterfact.html. NASA/JPL’s value for Jupiter’s orbital period is 4,3332.589 days. This differs by about 6 hours from the duration of the Jovian orbital period computed using the Babylonian “exact period” of ((427/36) ·365.256 =) 4332.342 days, which is 11.86 years.
[16] We assume the Babylonians didn’t spend much time on questions they couldn’t answer. But instead, being empiricists, looked at their data and saw that the longer arcs were in one part of the orbit and the shorter arcs in another. Clearly, Jupiter was moving faster in the longer arc, in one part of the sky, and slower in the shorter, in another part of the sky. What is additionally noteworthy among these early thinkers is what they did about it: they used the arcs as model templates to improve their predictions of Jupiter’s movements.
[17] For comparison, take the case of Mars. Its mean synodic arc is 48.72 degrees, indicating a mean shift of about a constellation and a half between each of the oppositions of that planet, occurring about every 778 days. Thus, over the course of three oppositions, the red planet’s apparent place in the sky will shift eastward among the constellations by about 49 degrees from first to second opposition, then another 49 degrees from second to third opposition, and so forth; at third opposition the planet will be about 98 degrees of longitude east along the ecliptic from where it was at first opposition. Applying these same principles to Jupiter, we would expect its arc to be shorter, which makes sense since it moves more slowly, and earth catches up with it more often for more frequent oppositions.
[18] A planet moves fastest near the sun (as it passes perihelion) and slowest at its most remote distance from the sun (at aphelion). For a planet with a sharply elliptical orbit (i.e., one having high eccentricity) the difference in orbital speeds at the ends or its orbit (or apsides) is greater than for one with a rounder orbit of lower eccentricity. The result of this difference, noticed by the Babylonians, is that the synodic arcs of Jupiter systematically vary in length from one part of the orbit to the other. Jupiter has a modest eccentricity, so its extremes are not too pronounced. But the keen-eyed Babylonians wanted to account even for these variations empirically, at least to a first approximation.
[19] HAMA, 375, 392 & 444. See also HAMA, 421 for System A’s parameters applicable to the other bodies in the solar system.
[20] HAMA, 398 & 442.
[21] HAMA, 392-393. The provenance of the tablet is given in ACT 339, also visible online at https://babel.hathitrust.org/cgi/pt?id=uva.x004508230&seq=77. This is the translated text, by Neugebauer. Portions of his transliterated text are in the header. The numbers are in sexagesimal notation. I've slightly enhanced the appearance of image for this article. Column I of the tablet gives consecutive years of the Seleucid era, beginning with (subtract 311 = ) ̵ 198. The left-hand column marked “Obv.” stands for “Obverse, or front of the tablet; “Rev.” is the reverse side. The first columns of numbers are the line numbers of the text. We are concerned here with Columns III, the date (showing months on the Babylonian calendar and day etc.), and IV, Jupiter’s longitude, shown in degrees from the beginning of the constellation denoted by the constellation's symbol, all of which symbols are shown on the right side of the header above.
[22] The synodic period on which the tablet is based is Jupiter’s first station. HAMA, 392. The Seleucid era began with the reconquest of Babylon by Seleucus I Nicator in 311 BCE, one of Alexander the Great’s Macedonian generals. He founded the Seleucid Empire. The Seleucid empire used the Babylonian Calendar in which the new year begins on 1 Nisanu (3 April in 311 BC).
[23] HAMA, 394. See also de Jong, 18, for his diagram of the synodic arcs of Jupiter plotted against ecliptic longitudes. His paper presents a thorough analysis of the origins of Babylonian planetary theory for the outer planets.
[24] HAMA, 394. In the four-zone model, the arcs were 30, 33;45, 36; and 33;45. The intermediate values allow for a smoother distribution and better fit for the arcs.
[25] In that spirit, I created a computer simulation of the Jovian synodic arcs in our era. I used NASA/JPL Horizons orbital elements (incorporated into a program I wrote with Maple mathematical software). The simulation plots Jupiter’s synodic arcs against time. It begins January 1, 2020, and continues forward several decades to 2042, about two Jovian orbits. The purpose was to help visualize the current changes in the synodic arc with modern data.
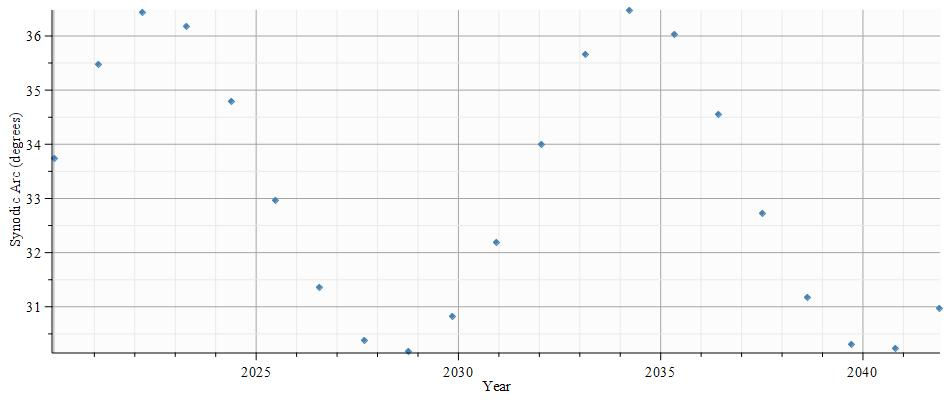
Here again we see the sinusoidal fluctuation of the synodic arc in degrees from about 30° to slightly more than 36°, with the mean synodic arc at 33.3°, consistent with what the Babylonians found and inscribed on their tablets 22 centuries ago. The two fast arcs in this small sample are above the median line and the slow arcs are below it. Jupiter will be moving most speedily in its orbit at perihelion, which will be at the peaks on the graph: one was in 2022, the other in 2034. The Jovian aphelion is in the troughs, in 2028 and 2039. The amplitude difference is 6.3 degrees.
[26] The title alludes to my June 14, 2021, post, A Farewell to Mars, and its chart called, “Babylonian Math on Your Calculator,” a summary of Babylonian arithmetical methods applicable to Mars.
[27] For fuller explanation, see the sources in note 4.
[28] HAMA, 391 & 441.



Comments