Alas Babylon! Mars Draws Near
- Douglas MacDougal
- Oct 1, 2020
- 4 min read
Updated: Oct 8, 2020

As Mars draws near, my thoughts turn to . . . Babylon. What’s this? Why Babylon? When the world absorbs the amazing photographs and data from spacecraft orbiting Mars, or marvels at the discovery of underground lakes at its south pole, teasing us again with speculations about life there, or when we just look in awe at the brilliant ruby star drawing so near, as it does every couple of years, why think about Babylon?
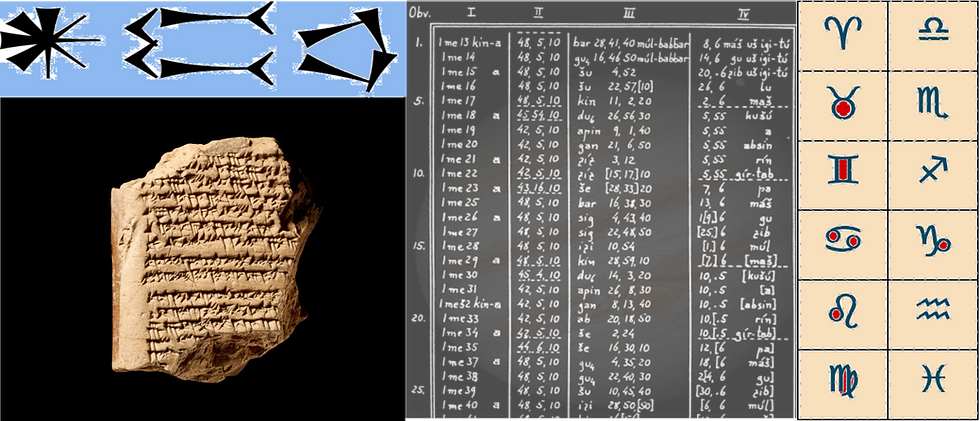
Here’s why Babylon fascinates me: It’s because the timing of these close encounters with Mars began with the Babylonians. Incredibly precise accounting of planetary positions started with them and lasted centuries. Indeed, computational astronomy began with them. The Babylonians started consistently tracking the positions of Mars and the other planets from about the mid- 7th century BC, and amazingly kept it up for another half millennium. These records are on about a thousand clay tablets mainly in the British Museum. As time passed, the Babylonians developed mathematical methods that allowed them to predict the planets’ positions and create ephemerides, even correcting for their variable orbital motion.
Let’s talk about the wandering star they called Nergal, the Greeks called the star of Ares, and the Romans called Mars. Over many centuries the Babylonians tracked Mars’s returns to the same position relative to the Earth and Sun. That alignment, the Sun-Earth-Mars lineup, occurs about every two years and fifty days. That’s about seven hundred eighty days. It’s known as the synodic period or synodic cycle. Any time Mars reaches opposition (opposite the sun), as it will on October 13, 2020, it will rise about at sunset. The Babylonians could not tell from observing Mars high in the sky, say at midnight, just when opposition occurred. But they noted its acronychal rising (evening rising) when the planet is last seen to rise after sunset.
Some get confused about this particular cycle, so let’s use a metaphor to help explain it. Suppose you find a unique analog clock – like the one that hung in your grandmother’s kitchen, only this clock is very different. Its two hands represent the movements of Earth and Mars around their orbits, and they move move counterclockwise at their respective mean speeds (with the simplifying assumption that they travel in uniform circular motion, not in ellipses). Let’s say they begin by being lined up at the ‘noon’ position (on a normal clock). The shorter hand moves with the speed of the Earth around the Sun, completing a revolution in three hundred sixty five and a quarter days. The longer hand moves with Mars’s motion along its orbit, rounding the center in about six hundred eighty seven days. The planets’ speeds are relative, so the clock units could be hours, minutes, or seconds, or whatever, instead of days. Around the edge of the clock face, where the numbers would be, are the constellations of the zodiac. The center of the clock where the hands meet is a small yellow circle, representing the sun. The plane of the clock face is the plane of the ecliptic.
When the planets’ hands are just lined up with each other, it is an opposition. We’ll call it a synodic event (you can hear the clock chime when the hands meet.) The synodic period or cycle is the interval between synodic events, and it’s about 780 days.
If Mars were standing still, its synodic cycle would be three hundred sixty five and a quarter days: Earth would simply pass it by, every year. If Mars were going half the speed of earth, the synodic cycle would be exactly two earth years. And in either scenario it would appear to return the same place – in exactly the same longitudinal spot along the ecliptic, in the same constellation in the sky – at every opposition. But Mars takes about 1.88 years to finish its orbit. That’s a year plus about eleven extra months for the hands to line up. So by the time earth has come around to a full year from the last opposition (the earth-hand swinging by the noon position) Mars is not there; it has moved on, its hand is about halfway farther around the clock face in our metaphor. After two complete earth circuits, faster-moving earth has almost caught up to Mars but needs another 1/7th of a revolution for the hands on the clock to line up and the clock-chime to sound. So with this extra seventh of a year, we should expect Mars to have advanced about a seventh of the way around the zodiac (again going counterclockwise) from each previous opposition, or more than a sign and a half along the twelve signs of the zodiac painted on the clock.
Now the Babylonians wanted to know how many synodic cycles would make Mars return to exactly the same place in the sky, in the same constellation, not a zodiacal sign-and-a-half away. They sought to know how many complete cycles would bring the earth and Mars to the very same place they started from. At such intervals, if they could be found, Mars would always be in the same place and in the same constellation as before. The hands would line up the way they did at the start (i.e., in our example, at the ‘noon’ position in our metaphorical clock). There were reasons for this as explained more fully in the PowerPoint attached below. One is that Mars was a malefic omen in Babylonian culture.
Finding an exact recurrence period for Mars isn’t possible, however, for the same reason that an irrational number cannot be reduced to a simple fraction.[1] But it is possible to find a recurrence period that is as close as we desire to get within any chosen margin of an exact return. And this is what the Babylonians did brilliantly. They found the recurrence periods shorter than a century for Mars and the other planets by about the 400 BC, and extrapolated their predictive ability by ingenious means to cover even longer spans of time. The attached PowerPoint explains a mathematical model I created to test one aspect of this amazing Babylonian achievement.
[1] The ratio of Earth’s and Mars’s mean periods in days, for example, is 365.25/686.98. That is an irrational number. You may check it. Here for your amusement are the first twenty digits: 0.53167486680834958805.


Comments