James Webb Space Telescope to Lift Off to L2 ~ But What’s L2?
- Douglas MacDougal
- Dec 16, 2021
- 11 min read
Updated: Dec 16, 2021
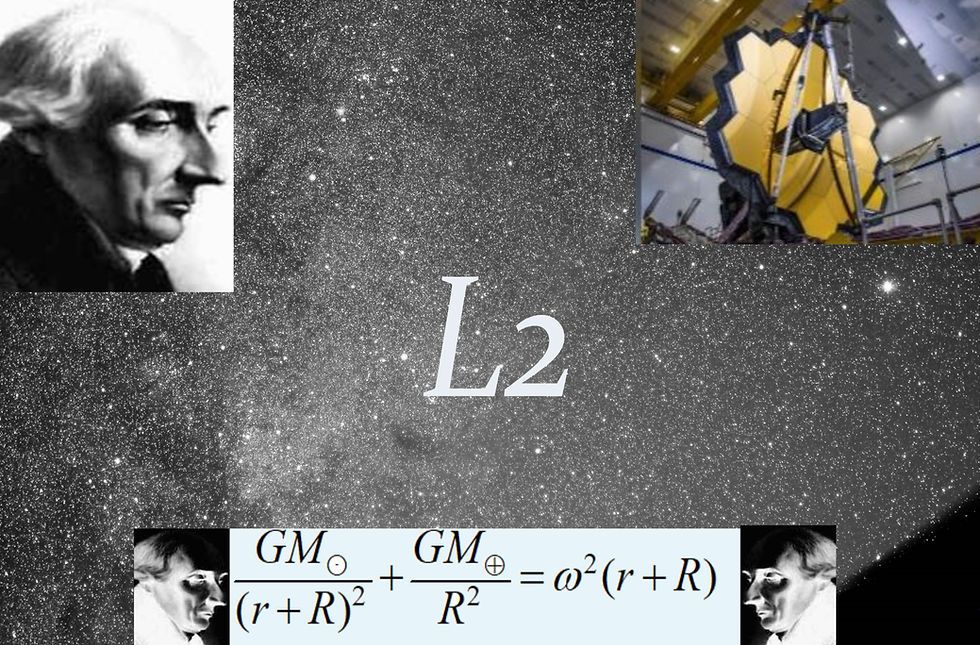
There’s a buzz of activity at the Arianespace's launch complex near Kourou, French Guiana. Finally, after so many delays, the James Webb Space Telescope is ready for its trip into space this month by an Ariane 5 rocket, the European Space Agency’s most reliable vehicle. After it’s up, JWST will spend a month journeying to the second Lagrangian point, the “L2 point,” where it will make its lasting home. JWST will hover in an orbit not around the Earth, as does the Hubble Space Telescope, but around the Sun. It will mimic Earth’s orbit but be some distance out from it, at the L2 point. It will also orbit around the L2 point, in a kind of perpendicular halo orbit with a six-month period, as the L2 point revolves around the Sun in lockstep with the Earth’s annual revolution. The Space Telescope will always look away from Sun and Earth. NASA tells us that the telescope will maintain a stable temperature out there, unaffected by passing in and out of the Earth’s shadow.
Yet some are puzzled by this unusual arrangement, and how it could even work. What created these magical, mysterious places in the sky that scientists always want to send stuff to? There’s nothing there, right? Others are vaguely aware of Lagrangian points but are in the dark about the not-so-simple physical theory behind them. All fair questions. To learn more, we’re going to take our own quick mathematical tour to L2. But first things first. Let’s find out what these funky points are and why they are so-called.
We’ll imagine asking the eminent Joseph-Louis Lagrange himself, the brilliant French mathematician and astronomer who was born in 1736 in Turin, Italy [1]. Though he died in 1813, he has graciously consented to answer a few questions for us. As moderator, I’ll let him do most of the talking.
Moderator: Professor Lagrange, I know you’ve been busy in new ways but glad you found time to join us. And you’re looking quite remarkably well, considering. Can you please explain your Lagrangian points to us, including the L2 point?
Professor Lagrange talks about his mysterious points
Prof. Lagrange: Oui! Time puts everything back in its place, non? Merci for allowing me to be among you, and for telling me about the wonderful progress you’ve made in celestial mechanics from where I left off two centuries ago. Consider three cases:
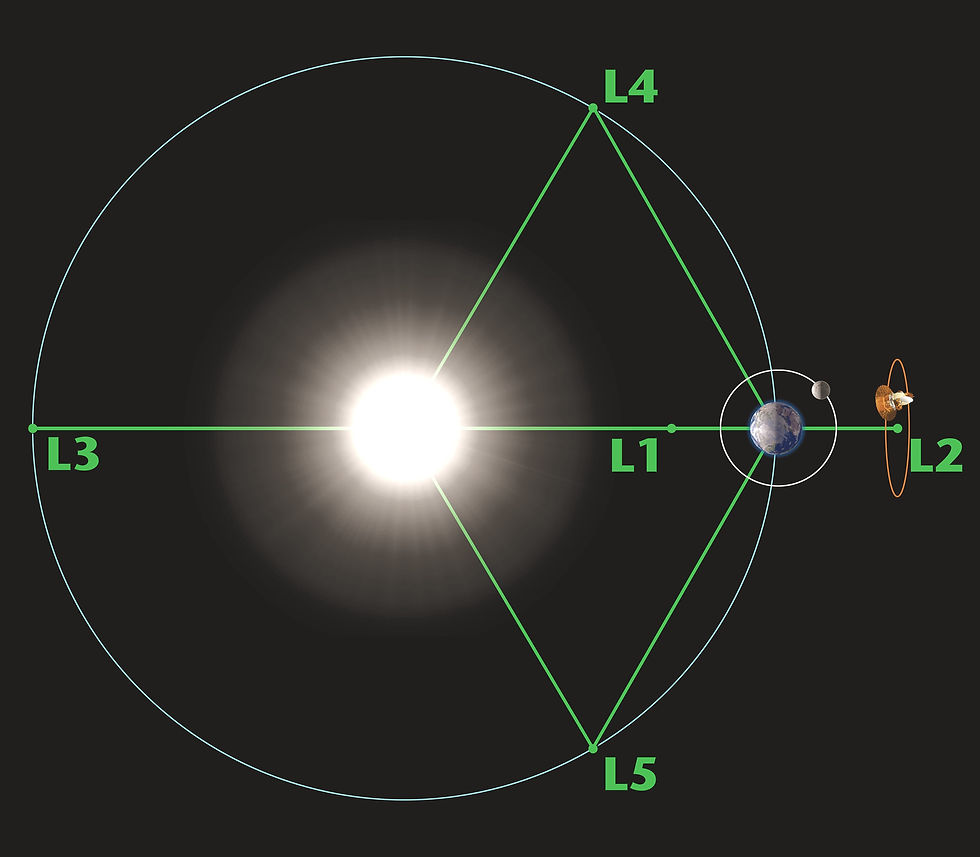
(1) Where the spacecraft is between the Earth and Sun, it is at the L1 point.
(2) Where it is outward of the Earth, it is at the L2 point.
(3) Where the spacecraft is opposite the Sun from us it is at the L3 point.
The L1, L2, and L3 points are all on the Earth-Sun axis. These, as I have shown, are points of only relative stability in any orbit.
Moderator: Are there other L points?
Prof Lagrange: I found two other points of greater stability on our planet’s orbital path, the L4 point, leading at sixty-degree angles from the Earth-Sun axis, and the L5 point, following at sixty degrees. They thus form an equilateral triangle with the Earth-Sun line. En effet, my Lagrangian points can be found in almost any three-body system. These stable areas are spots where solar system objects can accumulate and remain for eons. The best examples, confirmed long after my passing, are the Trojan asteroids clustering at the L4 and L5 points in Jupiter’s orbit. Here's a clear image your moderator modified from NASA showing the L points:
Moderator: Come to think of it, professor, NASA just launched the Lucy mission in October to explore Jupiter’s Trojan Asteroids at both L4 and L5 points. It will reach four of the Trojan L4 asteroids: 3548 Eurybates (which has a tiny moon, Queta) and 15094 Polymele in 2027, and 11351 Leucus and 21900 Orus in 2028. Then Lucy will make a graceful arc to the other side of the solar system to spy on the much larger binary Trojan asteroids 617 Patroclus and Menoetius in 2033 (binary because they orbit their common center of mass). The name Lucy comes from the australopithecine skeleton discovered in 1974 revealing early secrets of evolution; it is hoped spacecraft Lucy will do the same for solar system evolution.
Prof. Lagrange: Mon Dieu! Quels miracles!
Student: I hate to interrupt, but sorry, Professor Lagrange, I’m confused. Thanks by the way for being here. What I am trying to figure out is: How can an object orbiting the Sun farther out from the Earth, in a larger orbit, keep up with us? We learned in school that bodies in more distant orbits move more slowly. We overtake the slower, outer planets as we orbit the Sun, and the inner planets outpace us. Why won’t the Space Telescope fall behind us if it is farther out?
The professor explains how his Lagrangian points work
Prof. Lagrange: Oh no, it will stay with us! But to know why requires more attentive understanding of my points. We will try a thought experiment to exercise our intuition before we stir up the pot with equations. And from some simple deductions we will assuredly glean deeper insights that will prepare us for the mathematics.
First, any object – even a spacecraft – at Earth’s distance from the Sun will also have Earth’s one year period, correcte? Remember, by Kepler’s remarkable Third Law, the period (cubed) is proportional to the distance (squared) from the Sun. So, if the distance is the same, the period is the same. Now let’s look first at the L1 point and suppose your country has put a solar-orbiting spacecraft into a smaller, more inward orbit, which we’ll assume for the sake of simplicity is circular. Venus moves with a quicker period than Earth, and Mercury is quicker still. The spacecraft’s orbital period would, like the inner planets, also be less than a year, its increased velocity counteracting the increased pull of the Sun tending to draw it inward [2]. The actual period would of course still be determined by Kepler’s Third Law.
But now let’s go one step more: What if the gravitational attraction of the Sun perceived by the space-faring craft were somehow made less? This could happen if the spacecraft is still close enough to Earth-Moon system to feel their gravity pulling it outward, offsetting the inward pull of the Sun, in effect, reducing its pull; so, from the spacecraft’s gravity-perceiving perspective, it feels the same net solar pull just as the Earth does. If the ship is poised at some as-yet unknown distance between Earth’s system and the Sun, the net gravitational acceleration acting on it could be reduced, so that the period of the spacecraft would not be as short as it otherwise would be that distance [3]. In fact, if its distance from Earth were just so – the L1 point – its period could in theory exactly match the Earth’s – it would keep up with the Earth exactly, like the camera car in one of your marathons. In that case, the sum of the positive pull of the Sun in one direction and negative pull of the Earth-Moon system in the other direction must equal the centripetal force necessary to keep the spacecraft at L1. The balance of forces will result in the orbital velocity necessary to keep the spacecraft’s inertia from carrying it off in a straight line into space, ’est-ce pas vrai?
Student: Ok I get that, but how would it work for something that is farther out from the earth, at L2, where the Space Telescope’s going to be? Is it the same principle?
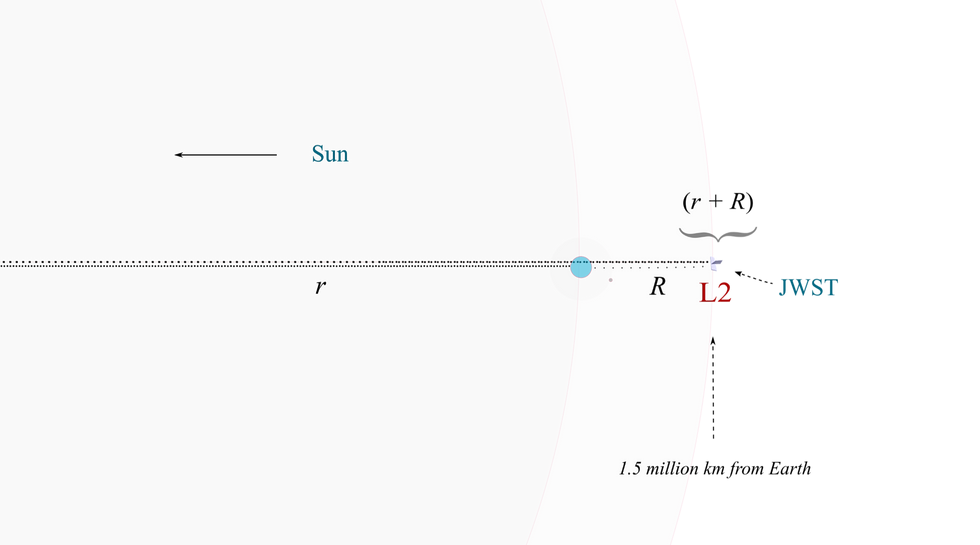
Prof. Lagrange: Exactement! A spacecraft or observatory such as JWST orbiting the Sun at a larger orbit than Earth would normally have a longer period than Earth (as in the case of the outer planets, all of which orbit successively more slowly). But if it were positioned just close enough to Earth so that the gravitation of the Earth-Moon system supplemented the Sun’s pull, then it would have a shorter orbital period than it otherwise would at that distance, i.e., were it experiencing the Sun’s gravity alone. At some particular distance – the L2 point – its period too would just match the Earth’s period. That turns out to be (as we’ll demonstrate) about 1.5 million kilometers farther out from the Earth’s orbit.
Moderator: I know we’ve done this before. The Wilkinson Microwave Anisotropy Probe (WMAP) launched by NASA in 2001 went to the L2 point and lingered in a halo orbit. It measured the cosmic microwave background (CMB) radiation from that thermally quiet environment. Other L2 examples I recall include the Herschel and Planck observatories launched by ESA back in 2009 and the ESA’s Gaia mission.
Student: Is it complicated to figure out exactly where these L points are?
Prof. Lagrange: No, but interestingly the study of my Lagrangian points yielded useful insights on how bodies orbit and interact in gravitational fields. While the interactions of two bodies are straightforwardly analyzed with Newtonian mechanics (the so-called two body problem), things become much more difficult when three or more bodies are involved (the three body problem). Many such problems cannot be solved by analysis but require computers that did not exist in my day to iterate approximate solutions. My Lagrangian points restrict the inquiry to certain spots in front and behind and to each side of a planet’s (or moon’s) orbit, where solutions are much simpler. Thus, it is an interesting form of what is known as a restricted three body problem. I’m sure you’ve read my 1772 prize-winning paper on this, Essai sur le Problme des Trois Corps. But we need to put pencil to paper to mathematically calculate where the points are.
He shows how to compute the L2 distance
To find the distance from Earth to the L2 point, we need to think of the applicable forces. Here we use Newton’s brilliant gravitational force equation which says the gravitational force imparted between two bodies is proportional to the product of their masses divided by the square of the distance between them [4]. All we need to do is calculate the gravitational force of the sun acting upon the spacecraft and add it to the gravitational force of the earth acting upon the spacecraft; their sum will tell us the total gravitational force pulling the spacecraft inward. The other equation tells us the centripetal force needed to buck its straight-line inertial force and hold it in orbit at the L2 point. Since we know its orbital period, we just need to find its distance out. We’ll equate the two forces to find the magical spot where it will neither fall in or fly off!
Student: Can you show us the actual equations please?
Prof. Lagrange: Oui. Let r be the distance between the Earth and the Sun, and R be the distance between the Earth and the L1 point that we want to solve for [5]. M is the mass (of Earth-Moon system or Sun, as indicated by the subscripts), and G is the Newtonian gravitational constant [6]. These numbers are in my notes below.
F1 is the Sun’s gravitational pull on a spacecraft at L2, at distance r + R from the Sun:
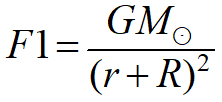
F2 is the Earth-Moon system’s gravitational pull on the spacecraft at distance R from Earth:
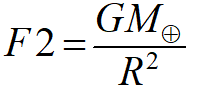
F3 is the centripetal force needed to hold something in circular orbit around the Sun at distance R from Earth:
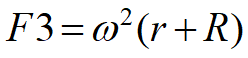
where ω is 4π/P, and P is the period of the Earth’s orbit [7]. Our task is to solve the equation F1 + F2 = F3. That is to say, find the distance R from the Earth in the direction opposite the Sun (the L2 point) where the gravitational and rotating forces are equal. In other words, we need to solve this equation for R:
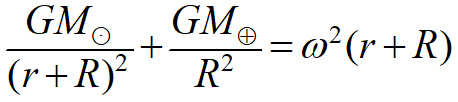
I find R is 1,512,000 kilometers [8]. That means that the L2 point is a million and a half kilometers outward from Earth, 180° away from the sun. This conforms to published data.
Student: I see. So, to find the L1 point, too, could we just use the same equation but reverse some of the signs?
Prof. Lagrange: Oui! All of the plus signs in the above equation become minus and you end up with the right equation to find the L1 point. Do you see why? I find R for the L1 to be about 1.49 million kilometers sunward from Earth. I am informed that the Solar and Heliospheric Observatory Satellite (SOHO) is there. See if you can come up with a formula for the L3 point on the opposite side of the sun.
How stable is the L2 point?
Moderator: Professor, can explain what you meant when you said the L2 point isn’t all that stable?
Lagrange: Bien sûr! First, let’s put some things in perspective. We know that while the Sun is massive (in kilograms, about 2 followed by 30 zeros) it is also far away – about 149.6 million kilometers distant from the Earth. And because gravity’s force diminishes with the square of the distance away, the actual acceleration perceived at our earthly outpost is modest. The Sun pulls on the Earth with a gravitational acceleration of only about .00593 m/s^2. That is, about 6 millimeters per second, every second [9]. That is Earth’s “free fall” acceleration toward the Sun. How can such a tiny pull keep our big Earth from travelling off into space? While this seems like a tenuous hold on our home, the Sun’s attraction is felt by every particle of the Earth, so the Sun’s net pull on the globe is about 3.54 × 10^22 newtons. It is this attraction on every particle composing our planet that keeps us in an orbital period of about 365¼ days. This solar acceleration is also slight compared to the Earth’s own gravity at its surface. The downward pull felt by you and me on the ground is about 9.8 m/s^2. This is about 1,650 times more than the 6 mm/s^2 gravitational acceleration from the Sun at Earth’s distance.
But by plugging in the R value back in the above equations – the distance from the Earth to the L2 point – we can see what the gravitational acceleration is for each component:

Differences in the acceleration of each component is on the order of less than a millimeter per second per second. So any gravitational perturbations that you can imagine will affect the position of the space telescope [10]. There are no strong gravitational limits there to prevent it from sloshing around a bit in L2 space.
Moderator: Thank you Prof. Lagrange for that excellent presentation! It is remarkable how slight is the contribution of the Earth’s own gravity to keep JWST on station at L2. The velocity differences are slight too. The Earth’s mean orbital velocity is 29.79 km/s. The mean velocity necessary to maintain the Space Telescope in orbit at the L2 point is 30.09 km/s, or only 300 meters per second faster. That’s an increase of only 1% of Earth’s orbital velocity. The extra speed works out to 671 mph, just under Mach 1. Your average jetliner at L2 could keep up with us!
NOTES
Top picture: Joseph-Louis Lagrange looking on. The equation is the one derived in the text for determining Lagrange's L2 point; its form is mine based on Lagrange's theory (the picture assumes he'd nod at it approvingly). The star field is a portion of a wide-field photograph of the southern sky in February. I took it a few years ago from the dark dark skies of Haleakala on the Island of Maui, altitude about 10,000'.
[1] Lagrange mastered and extended Newtonian mechanics, and in 1788 published his most famous work, Mécanique Analytique (Analytical Mechanics) after 35 years of effort.
[2] In terms of the principle of conservation of energy, the increased kinetic energy of the spacecraft (determined by the square of its velocity) offsets the (negative) gravitational potential energy of the Sun (determined by its distance from it) minus that of the Earth (also determined by its distance from it).
[3] The square of the period of an orbiting body is proportional to the cube of the distance and inversely proportional to the net gravitational pull on it. So for a given distance from the Sun, the greater the net gravitational pull, the shorter the period; the less the gravitational pull, the longer the period. To keep the periods the same, as we do when working with L1 or L2, one must either decrease the distance from the Sun if the net gravitational pull is less (the L1 scenario); or increase the distance from the Sun if the net gravitational pull is greater (the L2 scenario).
[4] The equation is F = GMm/r2 with the little m being the secondary mass here. We ignore the mass of the spacecraft because, no surprise, it is completely dwarfed by the mass of the Earth and/or Sun.
[5] The distance r is the astronomical unit. It is 1.496 x 1011 meters. R is the unknown that we are solving for. We are employing the simplifying assumption throughout that the orbits are all circular.
[6] Mass of the Earth-Moon system is 6.0471 x 1024 kg. Mass of the Sun is 1.9891 x 1030 kg. G = 6.674 x 10-11.
[7] We are using the MKS system, so the period of the Earth's orbit in seconds is, 3.155811840 x 107. This equation can be derived from the centripetal force equation discovered by Christian Huygens, F = mv2/r.
[8]1,511,993.793 kilometers by my calculation, with the assumptions and constants noted.
[9] This can be readily calculated from the Newtonian equation for gravitational acceleration, f = GM/r2.
[10] Nor, again, have we considered the eccentric orbit of the Earth, where the Moon is in its orbit, the variation in solar accelerations at the L2 point at different times of year and so forth.


Comments